Matrix operations are central to various fields such as data science, machine learning, and engineering. Python’s powerful libraries make these tasks seamless and efficient. One such library is NumPy, which stands for Numerical Python. This is an essential tool for anyone working with arrays and matrices in Python. Whether you’re enrolled in a Python learning course or just exploring on your own, this blog post will guide you on How to do Create a Matrix operations Using Python NumPy, giving you a solid foundation for solving complex mathematics effortlessly.
Why is NumPy used for Matrix Operations?
NumPy is highly optimised for numerical computation, making it faster and more efficient than standard Python lists. Using NumPy, you can:
Perform element-wise operations on arrays.
Use built-in functions for matrix operations.
Work with big data easily.
Enjoy support for multidimensional arrays.
Installing NumPy
Before diving into matrix operations, ensure you have NumPy installed. You can install it using pip:

Creating Matrices in NumPy
To start with matrix operations, you must create matrices. In NumPy, matrices are typically represented as 2D arrays.
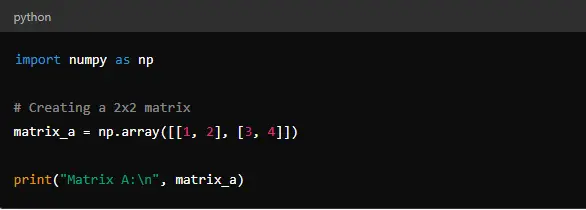
This code creates a 2×2 matrix ‘matrix_a’ with elements 1, 2, 3, and 4. The ‘np.array()‘ function is used to create arrays in NumPy.
1. Matrix Addition and Subtraction
Matrix addition and subtraction are straightforward in NumPy. You can simply use the ‘+’ and ‘-‘ operators.
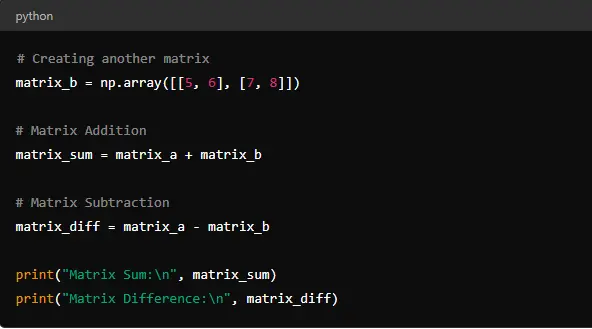
Here, ‘matrix_sum’ will be the result of adding ‘matrix_a’ and ‘matrix_b,’ and ‘matrix_diff ’ will be the result of subtracting ‘matrix_b’ from ‘matrix_a.’
2. Matrix Multiplication
Matrix multiplication is a bit different from element-wise multiplication. In NumPy, you can use the ‘np. dot()’ function or the ‘@’ operator for matrix multiplication.
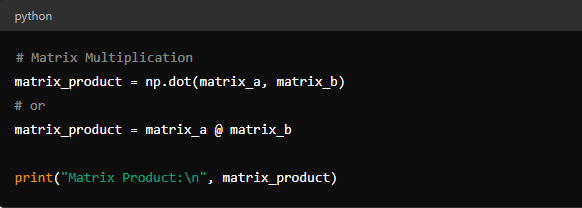
This operation follows the rules of linear algebra, where the number of rows in the first matrix must match the number of rows in the second matrix.
3. Element-Wise Multiplication
If you want to multiply the corresponding elements of two matrices, you can use the ‘*’ operator.
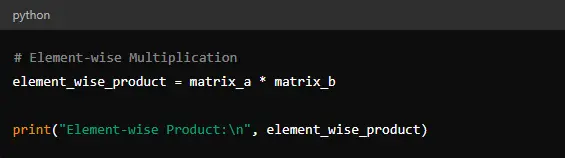
This will multiply each element of ‘matrix_a’ with the corresponding element in ‘matrix_b.’
4.Matrix Transposition
You obtain the transpose of a matrix by swapping its rows with its columns In NumPy, you can transpose a matrix using the ‘ T ‘ attribute.
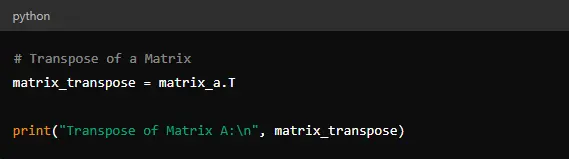
This code transposes ‘matrix_a,’ turning its rows into columns and vice versa
Advanced Matrix Operations
1.Matrix Inversion
The inverse of a matrix is a matrix that, when multiplied with the original matrix, yields the identity matrix. You can find the inverse using ‘np.linalg.inv().’
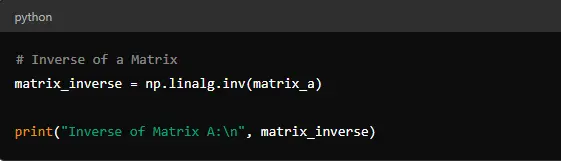
This function computes the inverse of ‘matrix_a.’ Note that only square matrices have inverses, and not all square matrices are invertible.
2.Matrix Determinant
The determinant of a matrix is a scalar value that is a function of its entries. You can calculate it using ‘np.linalg.det().’
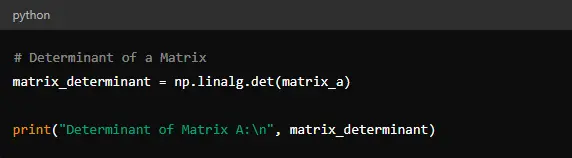
The determinant is useful in solving systems of linear equations, among other applications.
3.Eigenvalues and Eigenvectors
Eigenvalues and eigenvectors are essential concepts in linear algebra. You can compute them using ‘np.linalg.eig().’
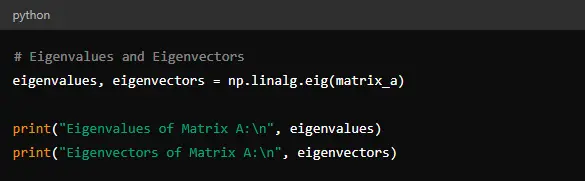
This function returns the eigenvalues and corresponding eigenvectors of ‘matrix_a.’
Check out the video to understand How To Do Matrix Operations Using Python NumPy
conclusion
NumPy simplifies matrix operations, making it a must-have tool for anyone involved in numerical calculations. Whether you are doing basic operations like addition and multiplication or more advanced tasks like matrix inversion and eigenvalue computation, NumPy has you covered. Understanding how to use NumPy for matrix operations will enhance your ability to work on data science projects, model machine learning, and solve complex mathematical problems. So, start taking action and incorporate Python NumPy into your work to harness the power of your projects. If you want to learn more or deepen your skills, consider enrolling in a Python data science course at GalTech School.







